标题太长了，其实它的全称是——给 geek 做礼物：Mathematica 和 Wolfram|Alpha Logo 折纸模型…无论如何也不知道应该如何化简了！

组合折纸

最近迷上了组合折纸（Unit Origami / Modular Origami），也就是折若干个一样的小单元，最后通过拼插，构造一个立体形状的折纸形式。刚开始是照着书来做，后来当然不满足于书上有限的几种组合形式，自己琢磨着做些新鲜玩意儿。于是是时候给我的“给 geek 做礼物”系列加一篇了！

至于做什么呢，今天要涉及到的是 geek 指数非常高的万能的 Mathematica 和强大的 Wolfram|Alpha。如果你家 geek 也是这两款产品的重度用户，那么做个 Mathematica 或 Wolfram|Alpha 的 logo 组合折纸模型送给对方是个不错的主意。这样你就不用花钱漂洋过海地去 Wolfram Store 买他们的纸模型了，况且折纸做出的模型听起来要比现成的更帅一点 :)

Mathematica 对本文亦有贡献（详情见文末花絮部分）。

Mathematica 和 Wolfram|Alpha 的 logo 是什么

想要自己设计一个组合折纸作品，首先要把一个形状进行分析，理解要完成的立体形状（通常是多面体）是怎样的一个构成，这样才能知道自己要折什么样的单元、折多少个。下面我们先来看看我们要折的这两个 logo 到底是个什么。

先来说 Mathematica 的 logo。

1988 年，Mathematica 诞生，如今已经发展到第 10 个版本。Mathematica 的 logo 也有个名字，叫做“Spikey”，每一个版本 Spikey 都发生了一些变化。下图所示的就是 Spikey 的 10 个版本。

可以看到，与版本 1 相比，后续的 Spikey 已经变得非常复杂，它们是将正十二面体的每个五边形的面修改为曲面得到的（具体的构造方法见这里）。我就不挑战曲面了，选择做最简单的 Mathematica 1。我们来分析一下 Spikey。

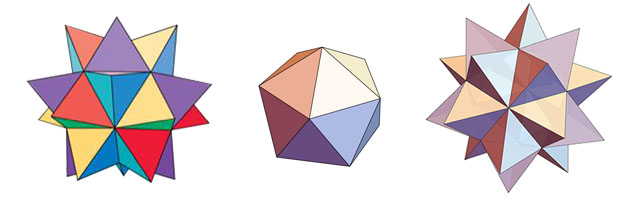
这个多面体可以这么理解：让正二十面体（上图中间的多面体）的每一个面上长出来一个正四面体，也就是以正二十面体的每个正三角形的面为底作正四面体，即可得到 Spikey。所以，Spikey 的表面总共有二十个正四面体，因此所有的面都是等边三角形，露在外面的面片数是 3 × 20 = 60 个。

由于正二十面体从每个顶点出发都有五条棱，很容易以此为基础构造出美丽的五瓣花瓣形图案，因此在组合折纸中，正二十面体的变体是最常见的结构之一。既然 Spikey 也是正二十面体为基础变化而来的，那么用组合折纸的方式做出它来也不是什么难事啦。唯一需要费点脑筋的就是正三角形的构造，用正方形纸折出 60° 其实不难，需要一点点初中几何知识。另外还有一点难办的就是还原它的颜色，我选择尽量遵循原版的配色，实在难以实现的部分用其他颜色代替了。

再来说 Wolfram|Alpha。

诞生于 2009 年的 Wolfram|Alpha 是 Mathematica 的同门师弟，因此 Wolfram 团队在想它的 logo 时，希望它既能让人联想到 Spikey 又带有自身的特色。Wolfram|Alpha 现在长成这个样子：

图中“WolframAlpha”字样前面的红红的多面体就是 Wolfram|Alpha 的 logo 啦，像一朵花一样，是从上百个方案里脱颖而出的最终赢家。这个多面体有一个名字，叫做 Rhombic Hexecontahedron（菱形六十面体）。顾名思义，它的每一个面都是菱形，总共有 60 个。

这个多面体也可以从正二十面体构造得出，不过稍微难想象一点。它其实是在正二十面体的每个三角形上长出来一个尖尖，这个尖尖是由三个菱形搭成的（如下图中间所示）。如果这样难想，我们就换一个角度，把它想成是正十二面体的每个五边形的面都捅进去一点得来的。至于两种思考方式为什么是一样的，大致是因为正二十面体和正十二面体是对偶的，正二十面体的每个面凸出来和正十二面体的每个面捅进去是一样的。

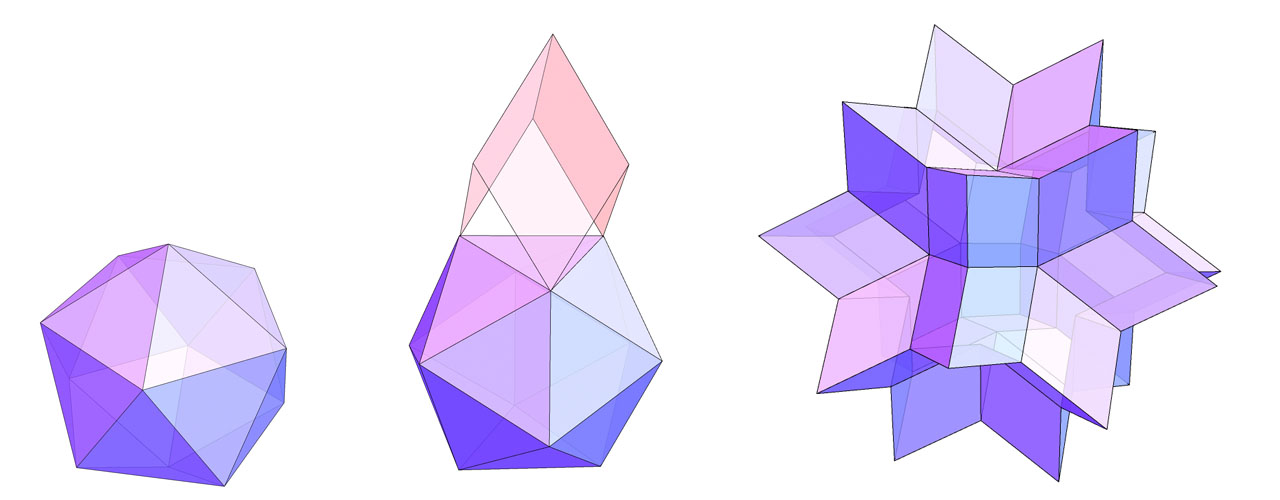
它的菱形也不是随随便便的菱形，而是一种叫做 Golden Rhombus 的菱形（黄金菱形），这种菱形的对角线长度之比刚好是黄金比例。比较头痛的是，要折出精确的黄金菱形有点难，好在黄金菱形的那个锐角度数大约是 63°，和 60° 非常接近，我就简化了一下模型，采用两个等边三角形拼成的菱形作为 Mathematica logo 模型的基本单元。它的折法和 Spikey 基本单元（等边三角形）是一样的，只是拼接上有些差异。

最后完成的两个模型是这样的：

铺垫了这么多，下面总算要开始讲怎么做了。想想到现在写了这么多，极有可能才占整个篇幅的 1/3，真有点懒癌发作想放弃。但这是三个月没有更新的人有脸做出的事吗！更何况后面才是我费最多力气准备的，咬咬牙继续嗯。

需要准备的材料

• 纸
• 裁纸刀（如果纸不是正方形的或者太大）
• 胶水（非必需，希望模型更牢固或初级选手可选用）

其实最重要的材料就是纸了。纸的选择和处理有几点注意事项：

• 这个模型的单元折法有点复杂，成品层数比较多，所以纸一定不要选太厚的
• 如果不用胶水，单元之间的连接刚开始会有点不稳定，稍有不慎就会脱节，最后完成了才会比较结实，所以纸最好不要太滑
• 纸越大越好折，但拼插起来会松散一些，小纸不好折，5 cm 已经很挑战我的大粗手指了，但成品很稳定
• Spikey 的单元我用的是边长 7.5 cm 的方形纸，Wolfram|Alpha 用的是 5 cm 的方形纸，最终成品大小差不多，直径在 9 cm 左右
• Spikey 需要 30 张正方形纸；Wolfram|Alpha 需要 60 张
• 最好直接买折纸专用纸，折纸规格是 15 cm 和 7.5 cm 两种，裁起来才不会太费劲

基本单元折法

组合折纸的特点就是重复劳动多，同样的单元要重复折出来几十个甚至上百个。但每个单元的折法其实并不复杂，有些极其简单，小朋友都可以轻松完成，但拼插出来的立体形状像万花筒一样有意想不到的效果，成就感满满，所以组合折纸应该会是一项非常有意思的亲子活动。

我们这次要折的单元在组合折纸中算非常复杂的一个了，因为要涉及到 60° 角的折叠。折法是布施知子在她的书中介绍的方法。虽然复杂，但重复 30 次甚至 60 次的时候就会慢慢熟练起来，我是折到第三遍基本脱离教程的，折到后面可以做到 30° 一折准，一边看电视一边折不用动脑子。

要开始了哟。

第 0 步. 一个竖直的折痕

如果是单面有颜色的纸，将有颜色的一面朝下。竖着把纸对折再展开。

折纸的过程中其实处处藏着几何。经常要以一些折痕为参考，进行后续步骤。所以折叠过程中会有折一下再展开的情况。这可不是多此一举。

第 1 步. 构造 60° 角！

以左下角为轴，翻折正方形的右下部分，使得右下角正好落在第 0 步折出的折痕上。

这样我们就得到了一个有一个角是 60° 的直角三角形（右图红色的部分）。为什么是 60°？看一下画出的直角三角形，斜边刚好是原正方形的边长，其中一个直角边刚好是上一步对折后的长度，也就是 1/2 个边长。直角边等于斜边的一半，30° 角就出来了。很容易得出来红色三角形的尖角也是 30°。这个折痕是我们后续步骤中重要的轴线。

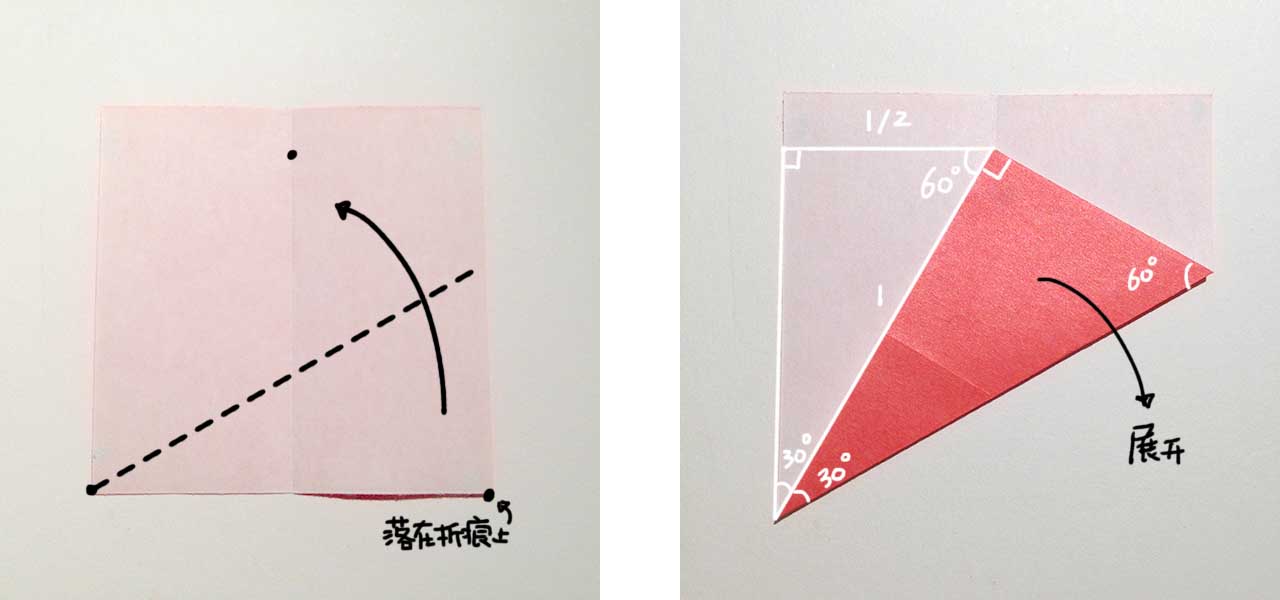
展开后，另一边也是同样的操作。

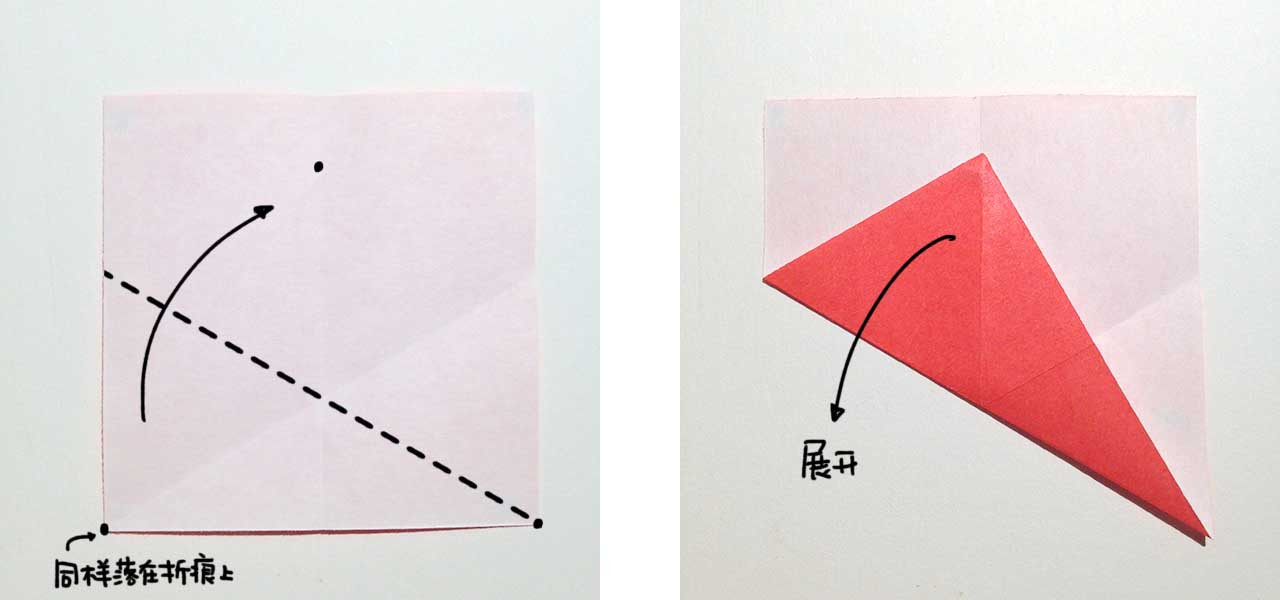
第 2 步. 菱形的两端

可以观察到，目前折出的三条折痕精确地交于一点。如果没有，要么是折得不够精细，要么就是纸不够方。最好能及时调整一下，因为越精确，拼插后的成品越漂亮。

将正方形的左下角折叠到交点处，右下角也做同样的处理。

展开后，正方形的底边产生了两个新的折痕交点。分别折叠正方形的两边，让左下角落到左边的交点处，右下角落在右边的交点处。这其实就是做了一个中垂线了，折痕应该垂直于正方形的底边，也就是平行于正方形的左右两边。剧透一下，这样折出来的宽度就是我们最终折好的菱形长对角线的长度了。

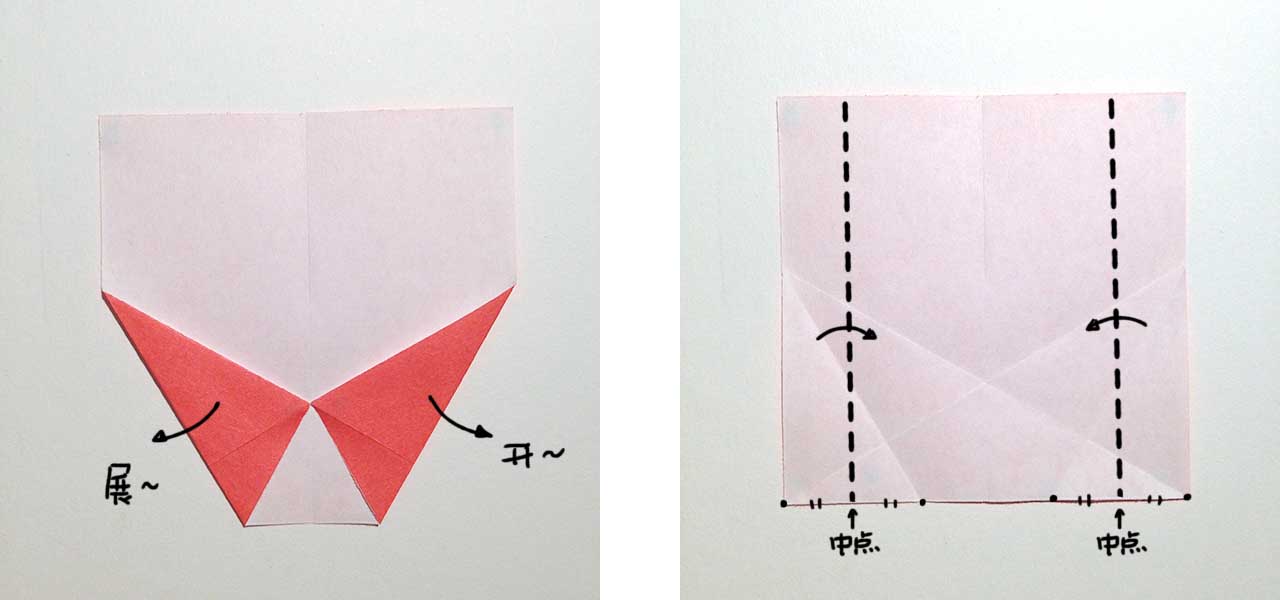
第 3 步. 菱形的边

观察右侧，接近中点的部分有一个折痕。以折痕与右侧边的交点为轴，将右上部分翻折到下面，对齐第 1 步折出的折痕。展开。

同理翻折左上部分，然后再如图向上对折。这个步骤中我们可以猜到哪些角是 60°，事实上至此，最终菱形的四条边已经构造完成了。

第 4 步. 一种有一点难度的展开

这一步涉及到一种新折法，叫展开。我们捏住图中所示的红色那一层向上翻开，这个过程中压住下面的白色部分保持不动。翻开后应该是右边的样子。再将右下角沿折痕翻折上来。

和前面一样处理，只不过是换了个方向。

第 5 步. 一种更有难度的展开

首先沿着中间的折痕对折整个图形，再展开。右图里可以看到一个等边三角形，那就是我们最终折好的菱形的其中一半啦。

接下来要进行一个比较复杂的展开过程，已经很难用文字和照片解释清楚了。大致就是捏住图中所示的位置沿折痕向左折叠，右上角的那一坨会自然地翻折下来。最后如下图的右边所示向上对折。

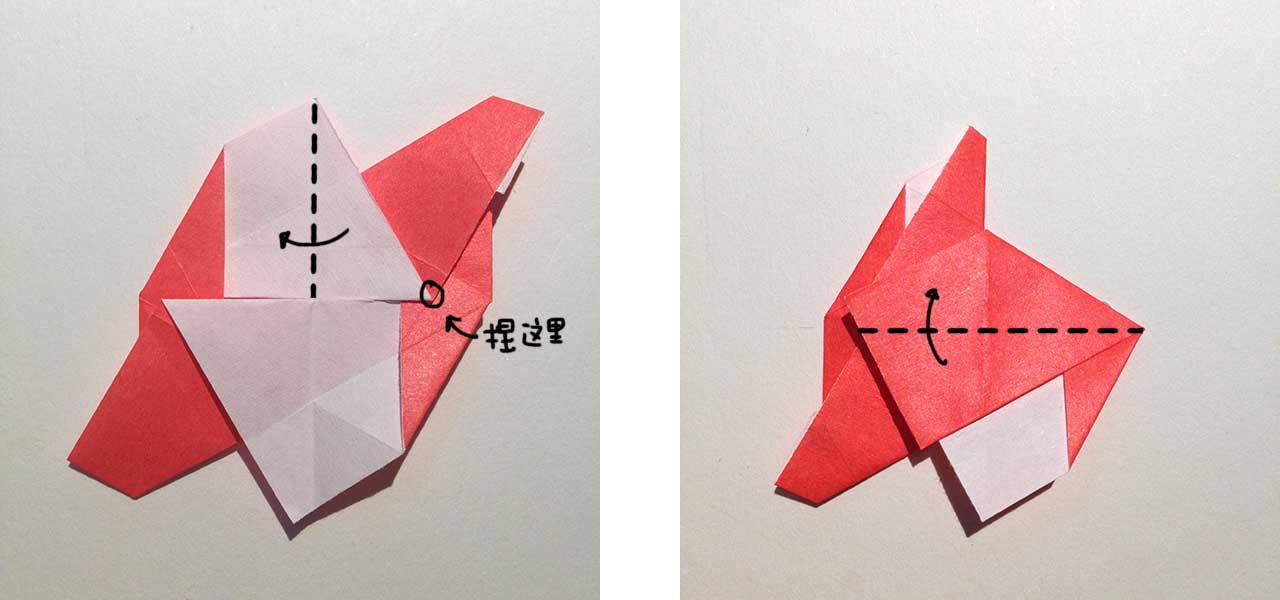
没看懂的话可以看一下下面的动态图，一遍又一遍地演示了这个过程（此处应该有掌声）。

第 6 步. “缝制”小口袋

首先我们要知道，组合折纸中，一个单元除了有它基本的形状（我们这里是那个菱形），还要有两个“口袋”和两个“触手”。口袋和触手是配套的，这样连接两个单元的时候，把其中一个的触手插进另一个单元的口袋，就连接好了。这一步中，我们就是给这个单元的口袋“缝”一个底。

把下图的阴影部分向后翻折，不仅要向后翻折，还要把阴影的小三角形塞到它后面那一层里。这一步一定要折得很牢固，因为这里就是口袋的“底”了，如果没有塞好，最后拼插的时候很容易跑出来。我们可以观察一下，现在右上部分实际上是两层，这就是口袋的“口”了，另一个单元的触手从这里进来。

下面的部分又要进行一次那个有难度的展开了。

虽然是同理，但勤劳的我还是做了一个动态图演示：

剩下的步骤也是一样一样的，只不过换了个方向。于是另一个口袋也完成了。

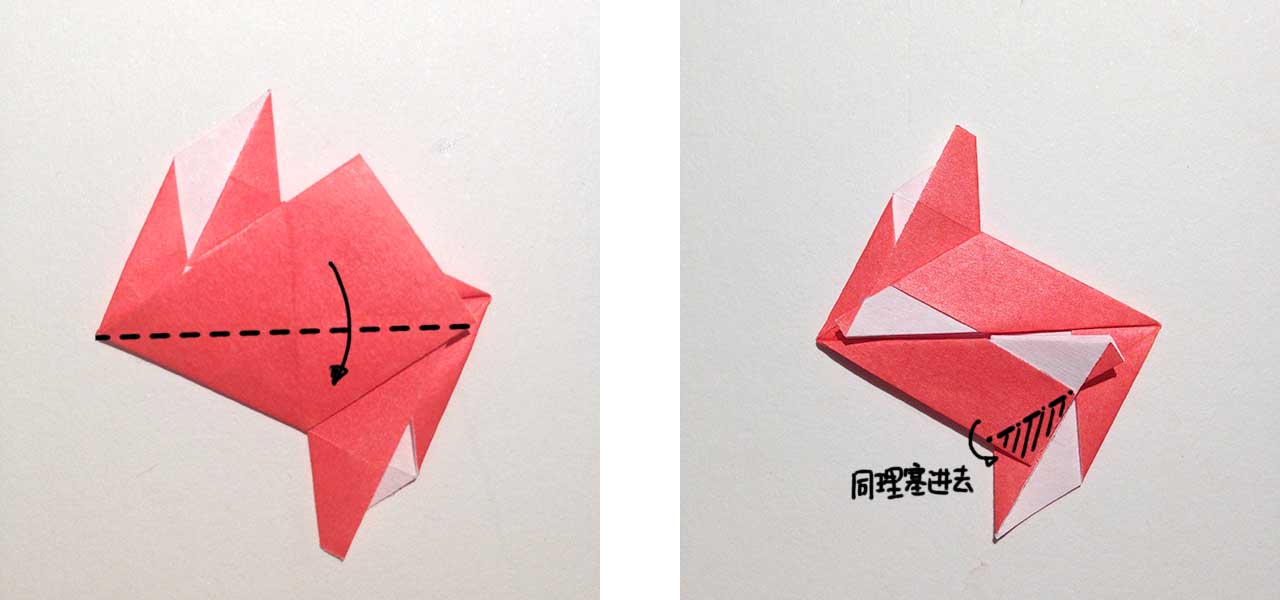
第 7 步. 加固、完成！

至此这个单元就基本做好了，但是还有些不听话的部分会翘起来影响最后的拼接，所以我们要把它们固定好。

就是下图圈出的这个部分了，我们把它塞到后面一层的小口袋里，这样它就老老实实地固定在那里，对折菱形的时候也不会轻易跑出来了。右边的也是一样的处理方式。

TADAAAA！终于完成了！虽然只是三十分之一或六十分之一，但是走到这里已经成功一半了。翻过来看，是不是看到了一个漂亮的菱形呢，你可以试着自己证明那个角的确是 60°。

最后附上一个完整折叠步骤的视频：

Spikey 的拼接法（制作时间约 1.5 小时）

学会了一个单元的折法，下面要开始更需要技巧的拼插环节了。我们先来看一下两个单元是怎么拼接到一起的。Spikey 的拼接需要先把单元折叠一下，像下图那样，把它对半折成等边三角形，并把三角形两边两个多余的部分一前一后折叠。拼插的时候，把一个单元的触手伸进另一个单元的夹层构成的口袋里，推到尽头。拼接完成后是下图最右边那样。

Spikey 1 的颜色挺多的，我尽量还原了它的配色，准备了紫色、红色、黄色、蓝色四种颜色（因为纸不够，每个颜色用了深浅两种凑数，大家没必要这样）。每个颜色 8 张就足够了，最后总共只需要 30 张纸，会剩下两张。

首先我们来拼正对着我们的那一圈，它由 5 个单元组成，两个黄色、两个红色和一个蓝色。像下图最右所示的顺序，按同样的方向一个一个拼插起来。这样由 5 个单元首尾相连拼出的“五元组”是这个结构的基本元素，现在一个主体就构造出来了，后面我们要一步一步为它增加新单元。

然后拼 logo 里那一圈紫色的五角星。折出 5 个紫色的单元，分别拼到图中所示的位置。每个新单元的触手要伸进主体的一个口袋中，同时主体上的触手要插到新单元的口袋里，这样一个单元才算拼插完毕。5 个紫色单元都这样拼好。这样我们已经拼好了 10 个单元。这是第一层，我们总共要拼三层。

下面，我们再来拼下一层的 10 个单元，它们会两两一组拼插到两个紫色单元之间。先来拼其中的 4 个，颜色、顺序和插入位置如下图最右所示。以蓝色红色这一组为例，拼插的顺序是这样的：蓝色的触手插进紫色的口袋，然后红色的触手插进蓝色的口袋，最后另一个紫色的触手插进红色的口袋。

插好之后如下图最左所示，可以看到画面里左上和右上都形成了一个“五元组”。前面讲到了 Spikey 是正二十面体的变体，所以它也和 5 这个数字有密切的关系。每一个凹进去的顶点，都应该有 5 个分支。

我们再来处理第二层剩余的 6 个单元，颜色和顺序也同样摆在图中了。拼插的方法也是一样，拼插好之后，应该又多了三个“五元组”。

现在两层已经拼好了，用掉了 20 个单元。我们把它翻过来，看到最上面一层歪歪扭扭的 10 个单元，就是我们上一步加进去的单元。在开始拼插剩余 10 个单元之前，我们先把它们化简。刚才说到 Spikey 的每个凹进去的点应该有 5 个分支，而它的每个尖尖的凸出来的点，则应该由 3 个单元构成。我们把第二层上每个紫色单元两边的单元再拼接起来，构成一个“三元体”。

接下来开始拼最后的 10 个单元。因为这里是背面，不会出现在镜头里，所以我不知道他们应该是什么颜色，就自暴自弃地随便用了剩下的颜色拼上去了，这种时候我就不去计较“柜子的背面也要用好木头”了…从这一步开始，颜色不具有参考意义。首先是用 5 个单元给第二层的 5 对单元“封口”，拼成 5 个“三元组”。

拼好之后，是不是有一种错觉感觉要完工了呢？其实这个“顶”还是虚的，我们还要用最后的 5 个单元，在顶上拼接出一个“五元组”，才算大功告成。注意，到了这个阶段，因为结构已经趋于稳定，触手直接伸进口袋会变得有难度，这时候需要把触手先折短一点再插到口袋里，这不会影响最后的成品。下图最右就是大功告成的 Spikey 啦！

Wolfram|Alpha 的拼接法（制作时间约 2.5 小时）

还记得 Wolfram|Alpha 的 logo 叫什么吗？菱形六十面体。所以我们需要做 60 个单元！全部用红色就可以了，做好之后自然会带有图中的光影效果。我的纸依然不够用，所以省吃俭用把一张 15 cm 的红纸裁成 9 张（人肉三等分很不容易的 T3T），还用了三个不同的红色才凑够 60 张。

Wolfram|Alpha 的拼接和 Spikey 稍有不同，因为它的基本面片是菱形的，不需要像 Spikey 那样对折单元，只需要把菱形两端多余的部分一前一后折好就可以了。它的拼插比 Spikey 要容易一些，但是牢固性稍差，可以考虑用胶水粘牢，或者前期用胶条辅助，全部插好之后再去掉胶条。

为了方便计数，我折单元的时候，每 5 个插好，像下图那样，这样 5 个一组 5 个一组数起来比较容易。最好一口气把 60 个都折好。这就需要将近两个小时的时间。

准备好之后，就要开始拼接了。菱形六十面体可以看作是 12 个“五角星”拼起来。所以我们就以 5 个单元为一组，首尾相连拼成下图最左所示的“五角星”。后面我们都 5 个 5 个进行拼接。

两个五角星拼好之后，我们将它们连接起来，每两个五角星会有两个角相连。第三个五角星分别和两个五角星有两个角相连。

同理我们拼插剩下的五角星们，只要遵循“每两个五角星有两个角相连”的规则，我们很快就能把 6 个五角星拼成下图最左的样子，这是整个模型的一个半球。剩下的半球当然是一样的道理，最后只需要把两个半球相连就可以了。相比之下，Wolfram|Alpha 的拼插难度很小，半小时之内一定能完成，主要的工作量集中在前期的单元折叠上。

 

花絮

0. 事情的起因 – Mathematica

凑单买了本组合折纸的书，然后就沉迷于此不可自拔。折多了发现这其中还是有规律可循的，不必非要照着书来组装。但自己发挥也不是那么容易，必须对多面体有一定的了解。这时候平时伺候起的智商外挂就派上用场了，他用 Mathematica  的 PolyhedronData 库调出来好多神奇的多面体供我参考。我看中了好几个非常漂亮的多面体，分析了一下可行性，似乎都可以实现。玩着玩着，我们发现了一个多面体的名字叫做 MathematicaPolyhedron，别名叫“Spikey”。知道它的身份后，它立刻成为了我的目标，决心挑战一下它。

就在我得意于自己的想法、兴致勃勃地自行研究如何改进现有单元为等边三角形的时候，一盆冷水泼了下来。顾森发来了一个链接，据链接里记载，早就有人做过这种事了！

有了先例，我自然就偷懒没有自己思考怎么去设计单元折法了，直接学习了链接里推荐的布施知子的折法。又研究了一番之后，我发现 Wolfram|Alpha 的 logo 也是可以用组合折纸完成的。

于是我和顾森兵分两路，我就去埋头研究怎么实现这两个模型了，而他则负责在一旁幸灾乐祸地找我想做的哪些模型都已经被别人做过了。时不时地他也会继续扮演“智商外挂”的角色，回答我冷不丁提出的诸如“能不能用三个颜色给正二十面体的棱染色，使得每个三角形面的三条棱颜色不一样”这种问题，或者给我解释某个折出来的角为什么是 60°，又或者用 Mathematica 做各种各样的图帮我理解多面体的构造。

本文和多面体相关的图示也都是托他用 Mathematica 做出来的，在此一并致谢。

1. 穿越感

为了让博客上的插图美美的，我特地把纸摆成下面这个样子拍了照片。就在我把照片发给顾森炫耀的时候，他沉默了不到一分钟，紧接着给我发来这个玩意儿！Mathematica 确实是个方便的东西，看到用它在不到一分钟的时间做出来的图，再看看自己花了好久才拍满意的照片，我觉得自己像是从远古时期穿越到现代的土包子。

这还不算完。在我解释我的照片是我怎么一点一点捻出来形状摆好拍出来之后，他又搞了张动图模拟了这个过程。穿越感再次袭击了我。

2. Matrix67 折纸作品赏析

左图：这个模型是由 A、B 两种不同的单元组合而成的，也是照着布施知子的书折出来的。他管我讨了 6 张纸，其中报废 2 张。

右图：为了验证我写的教程能不能看得懂、教得会，他作为小白鼠按照本教程折出的单元。

3. 事情的结局

• 我的彩纸多次出现不够用的情况，我只能可怜巴巴地一张纸裁成九张用。于是一天晚上，顾森扯着我去 MUJI 买了八包折纸专用纸。
• 顾森闲来无事翻看我的折纸书，最后竟然给初中学生上了一节折纸课，每个人折一个单元然后拼起来，顺带讲解这其中的几何知识。
• 我花巨大的精力做出来的立体球球们的最终待遇如何呢？有没有装在玻璃箱子里供起来？当然是沦为了猫玩具！
• 顾森为了应付我时不时提出的问题，补起了多面体的知识，结果水越来越深，目测他已经走火入魔。这两天废寝忘食地在看相关的资料，还用 Mathematica 做出来各种各样奇怪的图形，不知道在搞什么名堂（Update: 搞出这个名堂）。